Faça o download do texto clicando aqui.
A conduta da ação – O desencadeamento das elucubrações, triviais ou fantásticas, despertadas pela tomada de consciência da chamada cibernética sugere alguma prudência. “Deem-me feed-back e informação que construirei um mundo!”. Porém, até o momento, nenhum destes tipos de pensamentos virtuosos conseguiram produzir outra coisa que não seja devaneios sem consistência, inúteis e incertos (como dizíamos antes da cosmologia de Descartes, ainda que fosse bem estruturada).
Contudo, para sermos prudentes corremos o risco evidente de reduzir o pensamento cibernético, seja a um quadro de disciplina acadêmica ou a um oficio designado ao uso de engenheiros, seja a um desfile [ribambelle] de problemas matemáticos pequenos ou grandes.
Na verdade, a intuição inicial de Norbert Wiener: é que a possibilidade de uma teoria da comunicação e do controle que seja por sua vez autônoma e universal, só parece ser um ponto de partida, mas não um programa. Falta ainda, apesar dos brilhantes resultados do começo, um princípio unificador.
Sem pretender saber totalmente o que seria esse princípio, iremos examinar algumas sugestões sobre o que pode ser feito para dar um sentido, outro que não seja puramente tecnológico, às pesquisas da cibernética.
Gostaria de fazer uso do emprego de algumas imagens, para simplificar e abranger o assunto. Podemos representar as tentativas de atribuir um nome próprio à cibernética ao Kyberneter, o piloto, como fizemos para traduzir tal expressão grega; nas palavras exatas de um marinheiro antigo: “Nos navios, diz Bougainville, a função do piloto é de observar se os timoneiros seguem exatamente a rota que o capitão lhe ordenou”. Pouco importa que possa existir várias formas de pilotagem, aqui o piloto é um intermediário: ele não possui a tarefa de governar, nem de fazer outros exercícios, assim como também não comanda; ele controla, regra os meios segundo o fim ordenado pelo capitão.
Um pouco menos metaforicamente, em tais situações intermediárias que foram debatidas até agora: na máquina como no animal, não se preocupa diretamente com os efeitos produzidos, mas com a organização dos meios empregados para produzi-los. Não precisamos mais querer remontar aos fins últimos, só nos preocupamos com a eficácia. Ora, esta preocupação ultrapassa de maneira evidente o estudo das máquinas e dos seres vivos individuais. Em toda ação há uma decisão do “capitão”, a moral se quisermos, uma execução técnica e um importante lugar intermediário ocupado pelo nosso piloto.
Iremos dizer, após tantas pretensões de extrapolações indevidas, que a cibernética é a ciência da conduta da ação? Não, evidentemente, ao mesmo enquanto os elementos dessa ciência não forem reunidos e ordenados. Mas é interessante observarmos como surge alguns delineamentos e como conseguimos estabelecer o problema de suas relações.
A especificidade do domínio intermediário, o domínio do “piloto”, tem sido frequentemente indicada. Descartes, querendo colocar tudo sob questionamento para se tornar o seu próprio capitão, confrontou-se de maneira direta com tal necessidade: “para não permanecer irresoluto em minhas ações, enquanto a razão me obrigasse a sê-lo, em meus juízos, e de não deixar de viver desde então de o mais felizmente possível, formei para mim mesmo uma moral provisória”[1]. É assim que fala em seus discursos “para melhor conduzir sua razão”, e entre as máximas de sua moral provisória vejamos a seguinte:
Ser o mais firme e o mais resoluto possível em minhas ações, em não seguir menos constantemente do que se fossem muito seguras as opiniões mais duvidosas, sempre que eu me tivesse decidido a tanto. Imitando nisso os viajantes que, vendo-se extraviados nalguma floresta, não devem errar volteando, ora para um lado, ora para outro, nem menos ainda deter-se num sítio, mas caminhar sempre o mais reto possível para um mesmo lado, e não mudá-lo por fracas razões, ainda que no começo só o acaso talvez haja determinado a sua escolha: pois, por este meio, se não vão exatamente aonde desejam, ao menos chegarão no fim a alguma parte, onde verossimilmente estarão melhor do que no meio de uma floresta. E, assim como as ações da vida não suportam às vezes qualquer delonga, é uma verdade muito certa que, quando não está em nosso poder o discernir as opiniões mais verdadeiras, devemos seguir as mais prováveis; e mesmo, ainda que não notemos em umas mais probabilidades do que em outras, devemos, não obstante, decidir-nos por algumas e considerá-las depois não mais como duvidosas, na medida em que se relacionam com a prática, mas como muito verdadeiras e muito certas, porquanto a razão que a isso nos decidiu se apresenta como tal.[2]
Essa passagem é ainda mais interessante para nós:
E isto me permitiu, desde então, libertar-me de todos os arrependimentos e remorsos que costumam agitar as consciências desses espíritos fracos e vacilantes que se deixam levar inconstantemente a praticar, como boas, as coisas que depois julgam más.[3]
Há nesse texto, quase profético, uma porção de noções que poderiam mobilizar o ciberneticista moderno: o acaso, a marcha errante, e, mais ainda, a hesitação e o remorso considerados como uma espécie de mal que deve ser curado e cujo remédio nos é oferecido: um método de conduta, uma prudência, uma moral provisória.
Pode existir uma ciência ou pelo menos uma pesquisa científica que ofereça os princípios de conduta da ação humana? Tal pensamento não é novo, tampouco a ideia de lhe associar a uma matemática adequada. Certamente faz dez anos que existe uma literatura científica abundante sobre o assunto, mas já há um pouco mais de trinta anos que apareceram as primeiras anotações nas academias: cem anos atrás Cournot e Poisson escreveram sobre o assunto (mas seus livros não foram lidos nem com tanta frequência nem com seriedade); além disso, apesar dos trezentos anos, Pascal e Fermat trataram do assunto da aposta. Talvez exista nesse domínio muito mais coisas antigas do que possamos acreditar.
Labirintos – Retomemos o apólogo do homem perdido na floresta: o homem perdido, o labirinto, primeiros temas. A própria noção de labirinto precisa ser estudada de perto: pois é misterioso, como seu nome diz, a tal ponto que a língua inglesa designa com o mesmo nome (maze) a perplexidade desta arquitetura, como se tudo o que nos confunde, tudo o que nos surpreende, tudo o que é misterioso e desafiador fosse um tipo de labirinto, algo que não podemos deixar de notar. Mas “um jardim com caminhos que se bifurcam”, como diz um poeta argentino, é um problema e também uma estrutura matemática. Encontramos uma literatura matemática sobre o problema: sair de um labirinto cujo mapa desconhecemos. Observamos que o conhecimento e a ação estão ligados: eu quero alcançar o objetivo, ou seja, sair, mas é no próprio percurso, na exploração que aumentarei meu conhecimento e o conhecimento progressivamente adquirido dirigirá minha ação posterior. É agora ou nunca para fazer uma reflexão, uma ação em retorno [feedback?], um circuito de troca. Há uma rede espacial, há um percurso temporal, enfim, há o que ocorre na cabeça do explorador que é a imagem do dois e o lugar em que se encontra: há aqui mais do que uma analogia. Encontramos a estrutura fundamental dos exploradores ciberneticistas.
Em qual lugar nos estudos matemáticos ouvimos falar sobre o labirinto? Detalhe bastante singular, encontramos com muita frequência, ao menos no passado, nas coleções aparentemente pouco sérias, nas coleções de “recreações matemáticas”. Depois do Renascimento, a matemática solicitada sobretudo no domínio chamado atualmente de física, encontrou alguma dificuldade no lado das ciências humanas e a matemática que não serviu diretamente às ciências da natureza encontrou um refúgio provisório na teoria dos “jogos”. Um refúgio embora provisório. Provisório porque observamos ao longo da história um grande número de tentativas de emancipação desta matemática vinda do entretenimento e um pouco diferente das matemáticas tradicionais. Essa promoção da diversão à dignidade de estudo sério ocorreu por vezes de forma muito lenta: por exemplo, no que diz respeito aos labirintos, ela durou séculos; por vezes, ao contrário, ela foi explosiva e possui uma data de surgimento: é o caso da talvez maior e mais importante para todos os tipos de ciberneticistas: em 1654, nasce uma matemática do acaso. “A maior revolução lógica depois de Aristóteles”, como dizia Cournot.
É importante observar que o primeiro problema verdadeiro da ciência do acaso, aquele discutido por Pascal e Fermat, foi um problema de decisão: jogadores concordam com certa regra e são obrigados a parar o jogo no meio da partida; em seguida, eles precisam repartir de maneira equitativa o montante das apostas sem que tal situação houvesse sido prevista pelas regras estabelecidas anteriormente. Trata-se de explicitar as consequências das cláusulas do contrato e, o que propôs Pascal, inventar técnicas básicas que deveriam serem desenvolvidas posteriormente para se tornarem o nosso atual Cálculo de Probabilidades.
Para acompanharmos o desenvolvimento autônomo do cálculo de probabilidades e suas aplicações à física, terminamos perdendo um pouco de vista suas origens e negligenciamos as possibilidades de uma teoria da conduta humana. Mas os desenvolvimentos recentes da estatística aplicada são um pouco mais jovens do que esses velhos problemas e não seria descabido associar o estatístico, a seguradora e o jogador como três representantes das atitudes do homem em sua luta contra os riscos e as incertezas.
Por outro lado, no começo de maneira mais tímida e fragmentária, depois de forma mais sistemática, observamos ser construída uma análise matemática de situações cujos diversos jogos da sociedade oferecem ilustrações cômodas: aqueles da busca simultânea de diversos objetivos não necessariamente compatíveis. Neste caso, o acaso é menos essencial: podendo até mesmo ser ausente, por exemplo, em jogos de xadrez, luta entre duas inteligências cujos objetivos são opostos.
A regulação de um combate – um tipo de aplicação dos princípios gerais da regulação – aquela que tem, aliás, desempenhado certo papel na criação das ideias e do vocábulo na cibernética – nos permitiria vislumbrar ampliações possíveis e até mesmo sem dúvida necessárias. Trata-se da artilharia antiaérea: um avião em voo se torna o alvo de uma “bateria”, uma instalação que inclui, além de canhões, aparelhos que conduzem seu tiro, ou seja, que recebe informações (indicações) referentes à posição e ao movimento do avião e lhes transforma em possibilidades de explosões eficazes em uma região determinada no espaço. O alvo é alcançado, pelo aparelho que conduz o tiro, quando o avião se encontrar efetivamente nessa região em que os projéteis poderiam terem sido explodidos. Portanto, podemos construir um mecanismo de regulação automática que compare a cada instante a situação real do avião e aquela das explosões que poderiam ser realizadas, corrigindo os cálculos de forma a assegurar a coincidência.
O problema assim colocado, embora envolva mais complexidade por causa da previsão necessária sobre os movimentos que podem ser realizados pelo avião durante o tempo em que o projétil demorará para atingi-lo, não é logicamente diferente do problema da regulação de um motor. Contudo, há uma diferença, ou melhor, um elemento apenas aparente nas regulações industriais que foge aos olhos dos menos informados. A organização de uma regulação supõe a definição precisa de uma finalidade: para o motor seria certo regime de velocidade, para o aquecedor seria certa temperatura, o que equivaleria à coincidência do projétil com o alvo no caso da artilharia antiaérea. Mas definir de tal forma o objetivo consiste em adotar o ponto de vista da artilharia. Para o aviador o objetivo é outro: escapar do fogo, exatamente o contrário do objetivo inimigo. Portanto, existem duas finalidades opostas.
Os exemplos bélicos são os que explicitam melhor os casos de duelo; no domínio industrial, tais situações são raras. Para aproximar os tipos de regulação estudadas no primeiro capítulo desse livro, precisaríamos imaginar, por exemplo, que os condutores da máquina quisessem sabotar o funcionamento do motor, ou ainda, imaginar uma clientela que procurasse maliciosamente criar desordem na regulação automática, o que só poderia ocorrer no caso de propagação e disseminação de palavras de ordem (todos liguem as lâmpadas exatamente no mesmo momento, etc).
Dessa forma, surge a ideia de que os problemas de regulação industrial são casos particularmente simples de problemas de organização, exatamente os mais simples, pois o conjunto da aparelhagem admite uma única finalidade.
Os problemas de regulação da organização social, política, econômica, mesmo em pequena escala, ao contrário do caso industrial, fazem com que quase inevitavelmente apareça uma multiplicidade de objetivos perseguidos. As ilustrações típicas e inevitáveis de tais situações são fornecidas pelos jogos em sociedade aos quais nos referimos comumente há um bom tempo como envolvendo imagens de atividade bélica ou comercial. Quais são as ligações entre a Cibernética e a Teoria dos Jogos?
A diversidade de objetivos perseguidos evoca inevitavelmente a luta, mas que também poderíamos pensar nos casos de cooperação.
Trabalho em equipe e concorrência – O senhor Couffignal disse muito precisamente a propósito de certas máquinas de calcular (mas poderíamos dizer igualmente para outras máquinas): “o que não é um calculador isolado… é um escritório de cálculo que a máquina pode substituir, ou seja, uma equipe de calculadores. E caso queiramos ainda pensar nos robôs, precisamos conceber a máquina não como um robô, mas como uma equipe de inúmeros robôs. O problema de gerenciar os órgãos de tais máquinas não é apenas um problema científico e técnico, é, sobretudo, um problema de organização científica do trabalho”.
Porém, qual relação existe entre a equipe e o duelo? A equipe mais unificada, num dos extremos, e o duelo, noutro dos extremos, são apenas dois casos particulares do tema geral da ação coletiva.
Organizar uma equipe consiste em assegurar a convergência das ações individuais e garantir a unidade do objetivo, o que não ocorrerá sem dificuldade. Não é difícil de encontrar toda uma série de tipos de atividades coletivas, desde a unanimidade perfeita à guerra sem rendição e representar todos os estados intermediários. Evoquemos aqui somente as diferentes formas de concorrência comercial cujas alianças são feitas e desfeitas segundo os acordos e os desacordos provisórios dos objetivos perseguidos por cada um dos concorrentes. Notamos, assim, que se a equipe ideal age “como um único homem”, ou seja, possui apenas um único objetivo, as equipes reais não deixam de mostrar e revelar desacordos particulares e tensões internas, duelos por causa da falta de coincidência entre os fins perseguidos por cada um de seus membros.
É ao filósofo e matemático Cournot que devemos o primeiro ensaio sobre teoria matemática da concorrência comercial: suas Recherches sur les príncipes mathématiques de la théorie des Richesses [Pesquisas sobre os princípios matemáticos da teoria das Riquezas], apareceram em 1838 e não tiveram muitos leitores em seu tempo. Nós podemos, muito esquematicamente, apresentar a teoria de Cournot do seguinte modo.
A venda de uma mercadoria depende de seu preço: na maioria das vezes, podermos prever que venderemos melhor quanto mais baixo for o preço. O benefício do vendedor depende, por outro lado, simultaneamente do preço da venda e do saldo debitado. Com o produto muito caro, vendemos mal, logo, existe pouco ou nenhum benefício; com o produto muito barato, vendemos bem, mas talvez com prejuízo. Por tentativa e erro ou cálculos anteriores, o comerciante pode pesquisar o preço que lhe seja mais vantajoso. Não se trata, contudo, apenas de vender barato e o preço da mercadoria não depende apenas de sua própria decisão, mas também daquelas de seus concorrentes.
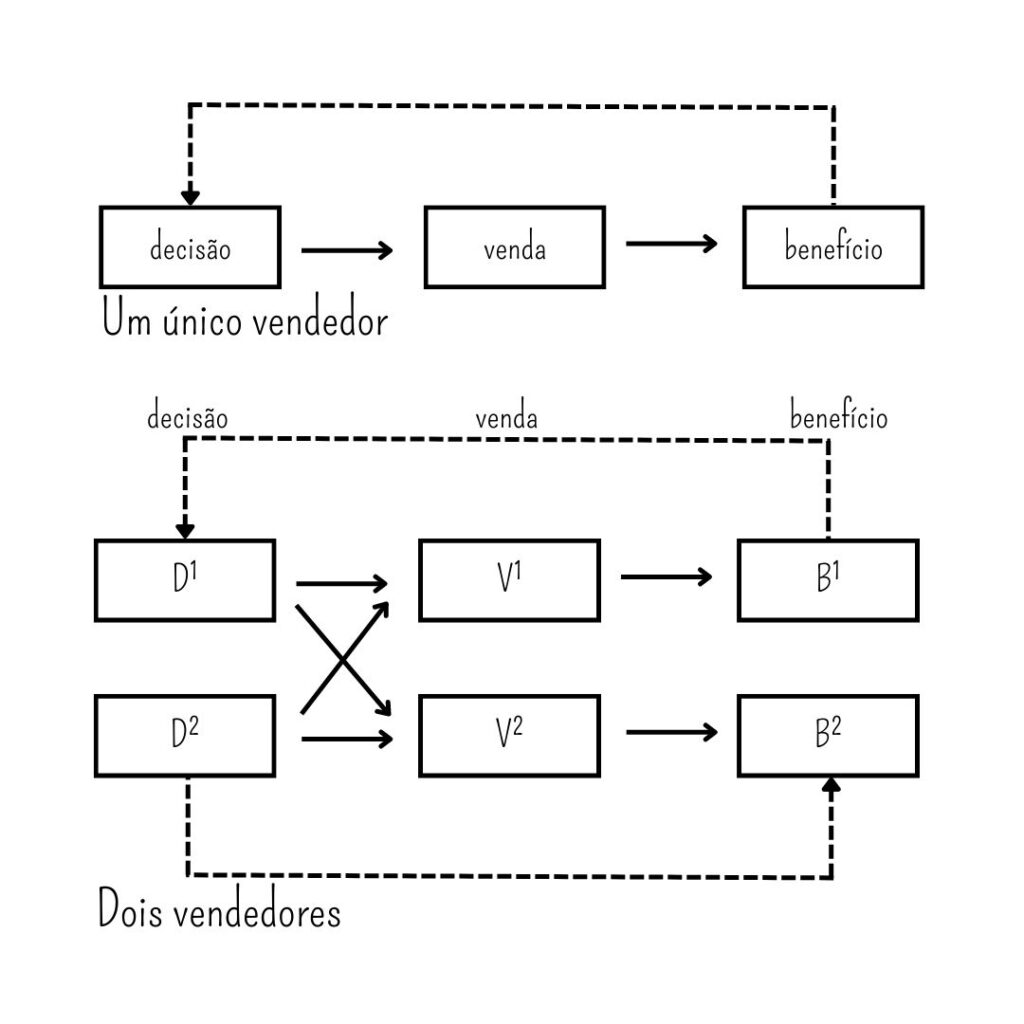
É necessário estudar as interações desenhadas no esquema precedente a partir das hipóteses convenientemente explicitas: por exemplo, supondo que o vendedor n°1 tomando a decisão D1 apenas se preocupe em aumentar seu benefício B1, sem se preocupar com o restante. Na sequência, poderíamos complicar o raciocínio e estudar o caso em que este vendedor busca prejudicar outro vendedor (ou seja, em que se preocupe com o benefício de B2), etc.
Portanto, é fundamental dizer de forma precisa quais são os meios da ação, ou seja, a relação entre a decisão e a venda (fixação de tarifas, publicidade, etc.).
Estratégias – Nestes diversos esquemas, aos quais não podem ser problematizados de maneira aprofundada aqui, trata-se certamente da ação humana, mas vista de certa forma incompleta, se preferimos. Mesmo quando os elementos psicológicos intervêm, eles não são nunca essenciais. Só nos preocupamos com a forma que as decisões tomadas por vários atores ligados por objetivos distintos poderiam reagir uma sobre as outras. E os esquemas construídos não poderiam ter a pretensão de esgotar o assunto, isto é, a inteligência da concorrência econômica e social. Tal atitude se aproxima um pouco da demografia quantitativa que não consegue exaurir o exame dos problemas da população, mas é um instrumento indispensável e preliminar; necessário embora insuficiente, para falar como os matemáticos.
Tais esquemas começam a prestar algum serviço ao serem relacionados diretamente a análise de operações (operation research) em contextos militares ou industriais. Porém, o fato é que este gênero de estudo parece se desviar absolutamente de toda aplicação às máquinas para só se concentrar em certos aspectos da ação humana. Isto é apenas uma aparência. Se o estatístico adquire hoje a imagem do jogador, é porque percebemos que não se limita apenas a calcular e raciocinar, mas que seus cálculos são feitos visando uma ação, cujo estatístico é responsável, ao menos parcialmente. Uma fórmula notável e frequentemente utilizada: “não há raciocínio indutivo, há apenas condutas indutivas”. O raciocínio indutivo pertence ao domínio, não da lógica, mas da ação.
A teoria dos sinais e da informação pode fornecer algumas ilustrações. Encontramos, como sabemos, no lugar central desta teoria a interação do sistema e do mundo exterior: a interação é aqui representada pelas alternativas inevitáveis e não completamente previsíveis cuja mensagem se encontra submetida em todos os processos de comunicação. É necessário não apenas tomar partido dessas perturbações, mas consegui dominá-las por alguma via. Além do mais, podemos até mesmo decifrar voluntariamente dessas alterações (criptografia). Encontrar o que poderíamos saber de uma mensagem que foi alterada por “ruído” é um dos problemas de base: é um problema de probabilidade. Wiener dedicou sua penúltima obra, segundo o autor, para revisar e unificar em uma base estatística técnicas de controle e comunicação, assunto cuja “filosofia” se encontra exposta no livro Cibernética. Quando possuímos o código, decodificar é uma tarefa “mecânica”, no sentido vulgar, e mecanicista, no sentido técnico. Quando não temos o código em mãos dizemos melhor que “deciframos”, estamos ainda em um problema de probabilidade. Toda tradução, digamos até mesmo toda leitura, está relacionada com um deciframento; não é perfeito o conhecimento das transformações da mensagem original, mas sua ignorância também não é total. Trata-se verdadeiramente do raciocínio indutivo de uma aposta. Em certos domínios bastante simples, a solução, deveríamos dizer decisão, sai do jogo de maneira bastante obscura, de intuições mais ou menos metodicamente enquadradas pelo raciocínio. Uma arte e não uma ciência, dirão os sabichões. A opinião vulgar admiti de forma bastante difícil que possa existir uma ciência das coisas incertas. E já fazem três séculos que Pascal protestaria contra esse prejulgamento. Àqueles que não enxergam “a regra da Aposta”, ou seja, o princípio de uma decisão fundada sobre um raciocínio probabilístico: “Todas essas pessoas viram os efeitos; mas não viram as causas. São, em relação aos que descobriram as causas, como os que só têm olhos em relação aos que têm o espirito.”[4].
Podemos identificar uma mudança análoga com o construtor de máquinas: se ainda sonha em se tornar por seus engenhos o “senhor e detentor da natureza”, estará tentado a reconhecer que não irá muito longe e será forçado a dizer: “a natureza possui boas defesas”. Não se trata de personificar a magnitude do Universo ou construir um “Diabo” científico, como diz divertidamente Wiener. Mas se queremos ser prudentes, é necessário prever o pior e calcular sua própria estratégia como se o obstáculo fosse um adversário.
Nós só podemos seguir aqui os desenvolvimentos recentes da teoria dos jogos de estratégia. Terá sido suficiente indicar desde já, no domínio técnico, algumas construções matemáticas destinadas a dar conta de conflitos humanos que encontram seu lugar natural nos problemas da organização.
[1] DESCARTES, R. Discurso sobre o método: para bem conduzir a própria razão e procurar a verdade nas ciências. São Paulo: Difel, 1962 p. 17.
[2] Idem, p. 18.
[3] Ibidem.
[4] PASCAL, B. Pensamentos. São Paulo, Abril cultura, 1984, p. 98
